Grace Teng

Layers of Abstraction

The essence of abstractions is preserving information that is relevant in a given context, and forgetting information that is irrelevant in that context. – John V. Guttag (from Introduction to Computation and Programming Using Python)

I started learning programming when I was 10, when I walked into my father’s study late one night and found him typing away using a program I didn’t recognise.

“What’s this?” I asked.

“It’s Visual Basic,” he replied. “I’ll show you tomorrow.”

The next day, he sat me down in front of the computer and showed me how to draw a button on a window in Visual Basic that would say “Hello World!” when I clicked on it. I was hooked. I was still a Windows user at the time, and being able to create my own program that looked exactly like a real Windows program was such a heady feeling.

There was one step I didn’t understand, though. Before my program would run, I had to compile it.

“What does ‘compile’ mean?” I asked.

“It means the computer has to turn what you’ve written into a language the computer can understand,” my dad said.

As I learnt more about programming, I heard terms like “assembly language”, “low-level” and “high-level”. I gathered that “assembly” was a low-level language, but when I asked my dad what that meant, he answered rather cryptically that a low-level language was “close to the CPU”, or something like that.

Ones and Zeros

In high school physics, we learnt about these things called logic gates, which always seemed rather out of place to me in the physics curriculum. We’d get a diagram like this:

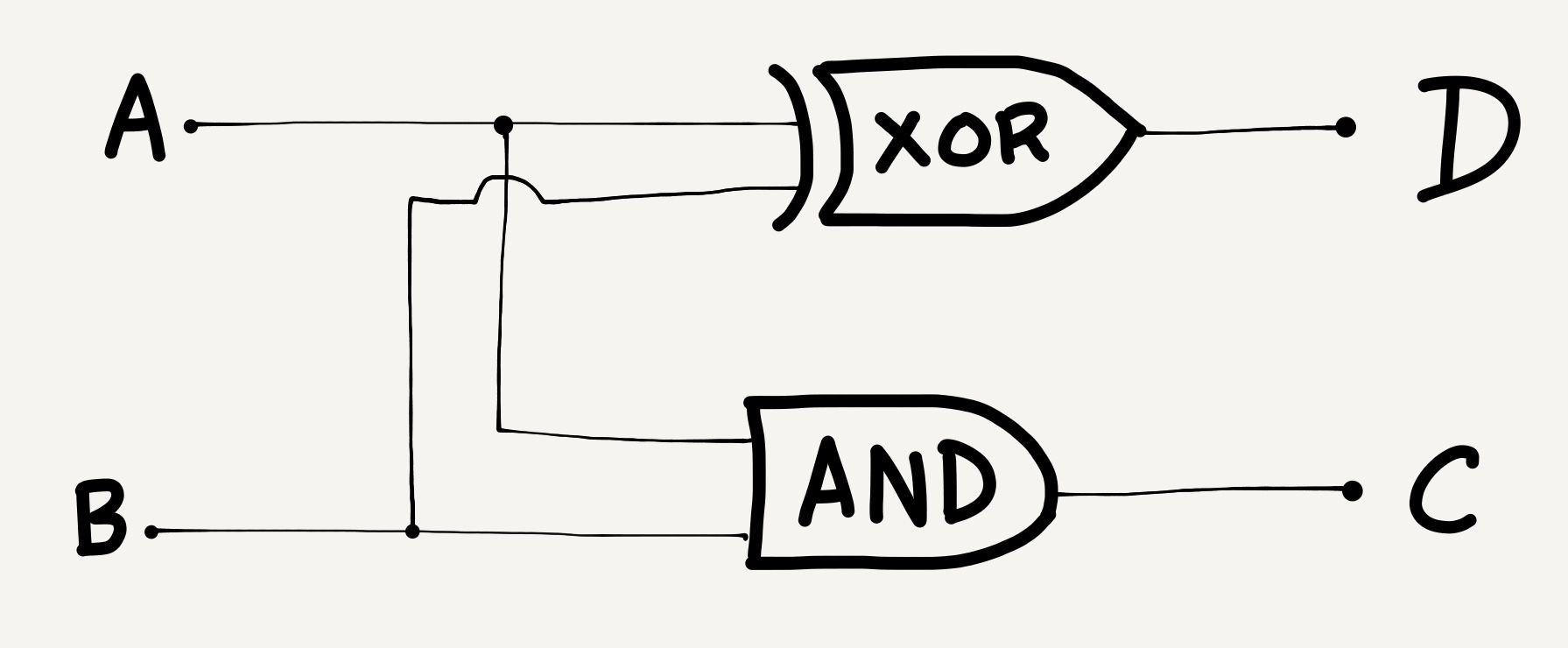A random circuit of logic gates

and we’d have to fill in a “truth table” like this:

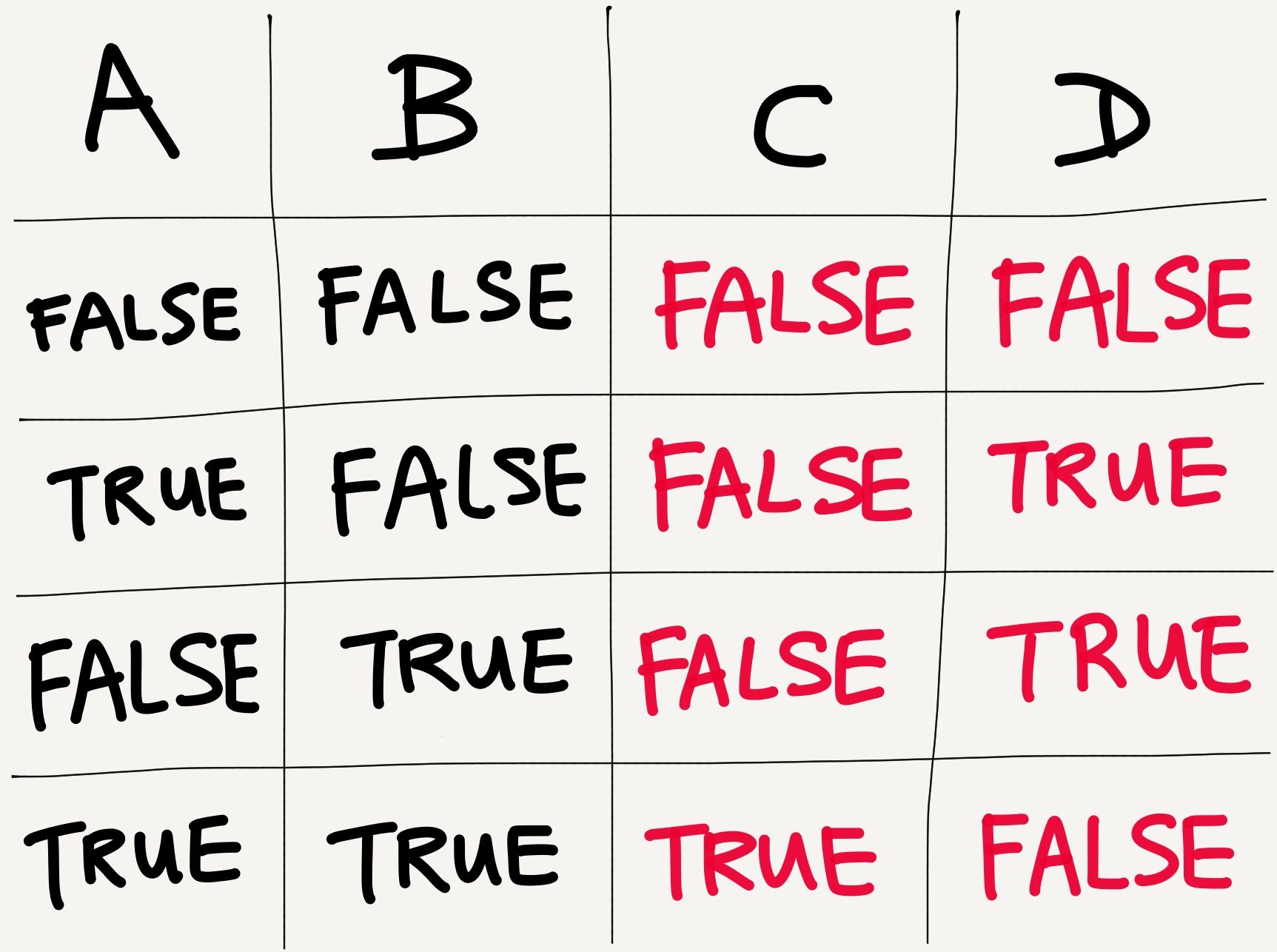Not much physics going on here… or is there?

The logic gate diagram consists of an XOR gate and an AND gate. Individually, these gates simply take two inputs, and give one output. The AND gate outputs TRUE if both its inputs are TRUE, and FALSE otherwise. The XOR gate outputs TRUE if both its inputs are the same, and outputs FALSE if its two inputs are different.

The thing is, we were working out truth tables for these abstract things called logic gates, but nobody in high school ever showed us what a logic gate looked like. If they had, we’d have understood that logic gates were electrical components, switches that turned low voltages (representing FALSE) into high voltages (representing TRUE), or that took two different voltages and produced a third, based on what those two input voltages were.

Because of this, the chapter on logic gates never felt like physics to me. All of it seemed to rest on an understanding of logic, not of physical phenomena. Logic gates probably snuck in there because logic gates are critical to how computers work, and presumably at the time the curriculum was designed, computer science was considered to be a subdiscipline of engineering, and was therefore a closer cousin of physics than of mathematics. Anyway.

What’s 1 + 1?

2, you might say. Well, you’d be correct in any number base except base two. In a binary number system, 1 + 1 = 10. Since a binary system has only 1s and 0s, you’d need to carry over the ones digit to the next column.

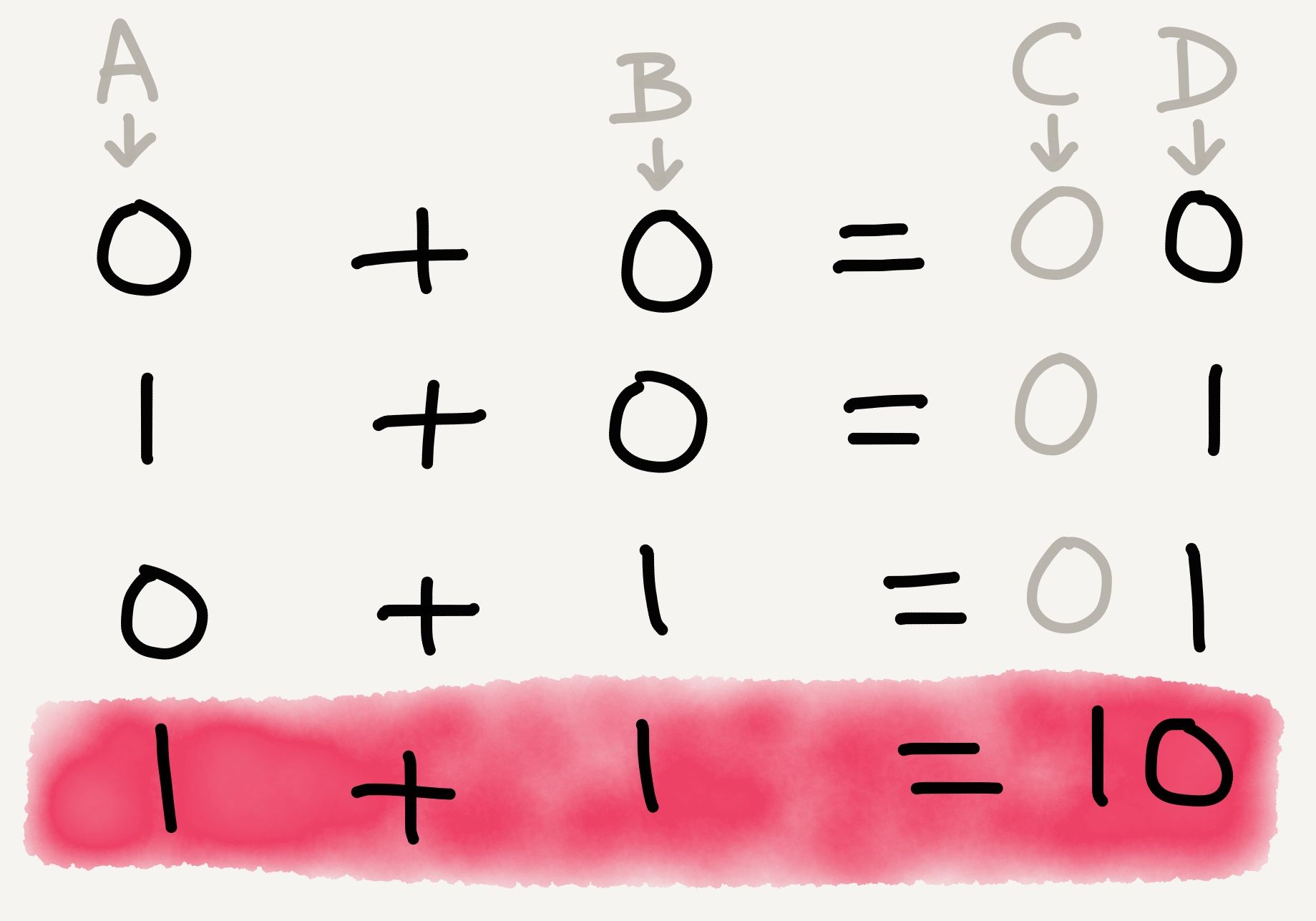Adding binary numbers together

If you take the truth table from the logic gate diagram above, and replace TRUE with 1 and FALSE with 0, you’ll arrive at precisely the binary addition table above.

And so, out of the elemental logic gates XOR and AND, we have built a half adder , a circuit that takes two binary digits and tells you the sum. It can only add 0 + 0, 0 + 1, and 1 + 1, but that’s okay; those are the only things you can add in binary anyway.

The beautiful thing about this arrangement of logic gates is that it doesn’t have to be thought of purely in terms of AND, and XOR gates. You can arrange two half adders like this, for example, to get a full adder , which lets you add three binary digits together:

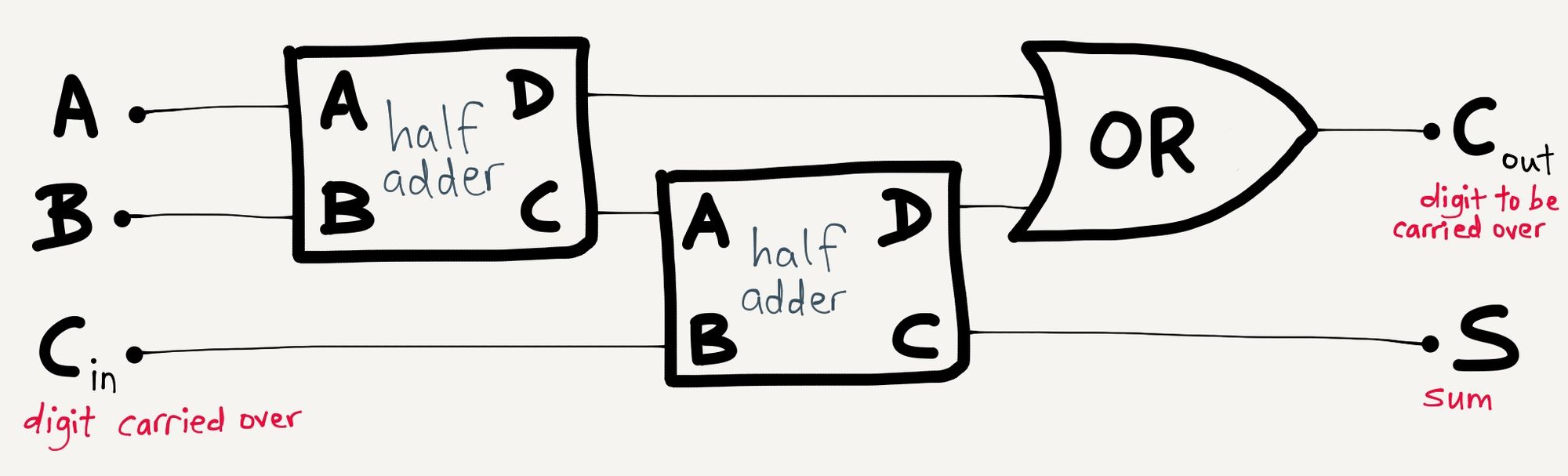Adding two half adders and an OR gate together

Then you can arrange full adders to make what are called ripple-carry adders , which let you add two binary numbers of any number of digits together. Here’s one that lets you add two 4-bit binary numbers together:

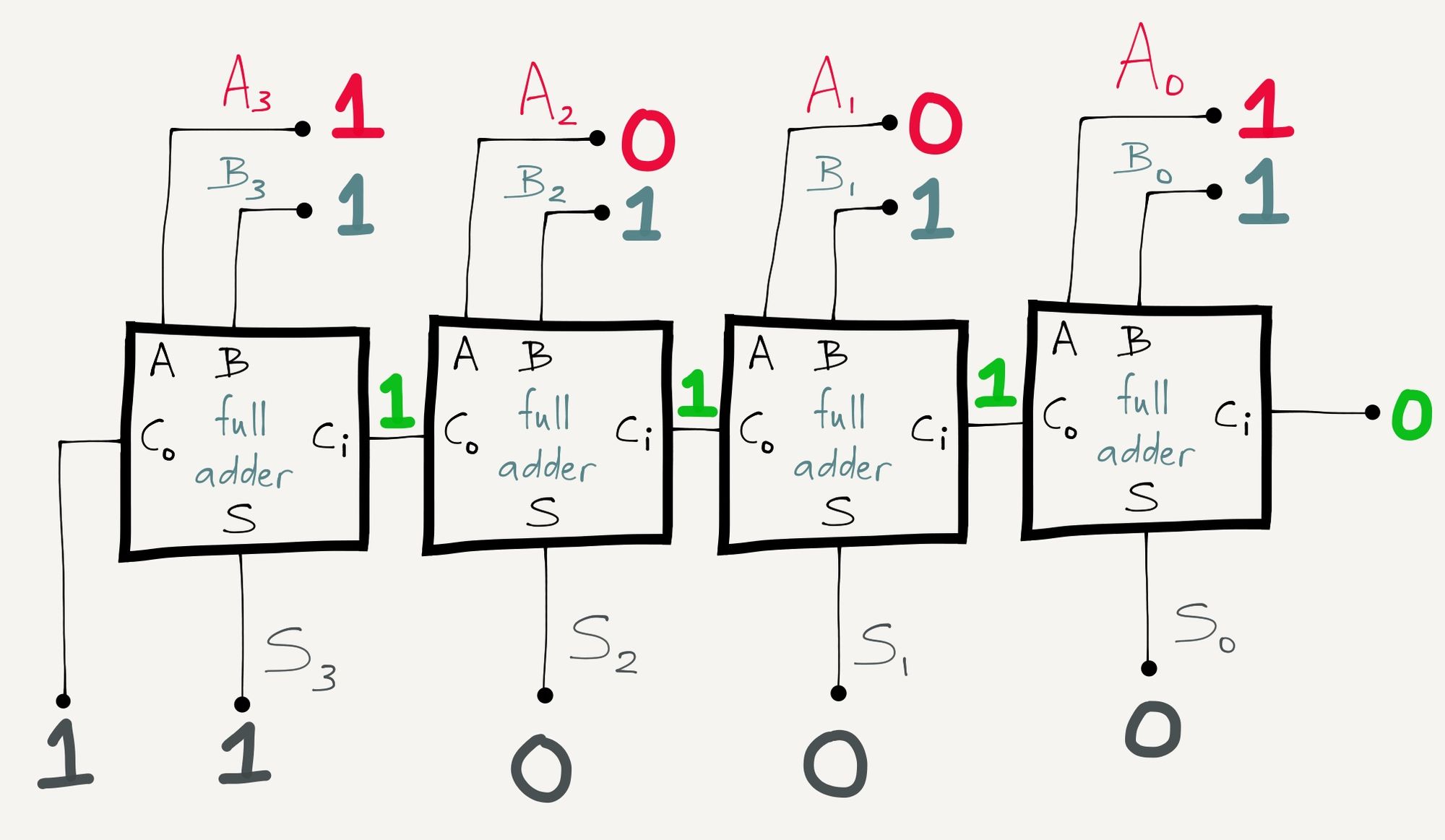Nine (1001) plus fifteen (1111) equals twenty-four (11000)

Look, that thing can add up to 1 + 15 + 15!

As you build more and more complex configurations of logic gates upon one another, you stop thinking about NOT, XOR and AND, and you start thinking about adders. Put many adders together and you get an arithmetic logic unit (ALU). Put many ALUs together and combine them with other configurations of logic gates, and eventually, you get a central processing unit (CPU).

Underlying all the computational power of today’s CPU is the humble logic gate, but by the time we’re thinking on the level of CPUs, we’re no longer thinking about individual logic gates. The logic gates themselves are no longer relevant. What’s relevant are the layers we’ve built above the logic gates that allow us to store and manipulate data.

Low and High Levels of Abstraction

Think about a typical desktop computer. It’s got a screen, a keyboard, a mouse, a processor and some speakers, at the minimum.

How many keys do you have on your keyboard? If you have a full-size 104-key keyboard, think about the minimum number of 1s and 0s needed to transmit any given keystroke. (Answer: eight.) Imagine your keyboard transmitting sets of eight 1s and 0s through the wire into your CPU, and your CPU sending that input signal through millions of logic gates, and spitting out another set of 1s and 0s in order to display that letter on the screen… the amount of computation involved would overwhelm the human mind. It’s a wonder we manage to get computers to do anything at all.

That’s not how most software engineers engage with computers, though. If programmers had to think about how to read individual key presses from your keyboard in this manner, we’d never have gotten word processors, Photoshop, or Counter-Strike. Fortunately, they don’t have to do that.

Engaging with the computer on the level of 1s and 0s is a really low-level way of operating. If you’re directly feeding the CPU 1s and 0s, you’re probably working with machine code. Machine code is so difficult to work with that there’s a mnemonic version, assembly language, that lets us write in something vaguely recognisable as human language. You write your code in assembly, run what you’ve written through an assembler, and the assembler spits out machine code.

This is what computer scientists and software engineers refer to as abstraction. In computing parlance, assembly provides a layer of abstraction on top of machine code.

Even assembly is unwieldy. The Wikipedia page for low-level programming language gives an example of a Fibonacci calculator written in x86 assembly (it should be noted that there’s no one “assembly language” — each CPU architecture has its own):

fib:
  mov edx, [esp+8]
  cmp edx, 0
  ja @f
  mov eax, 0
  ret

@@:
  cmp edx, 2
  ja @f
  mov eax, 1
  ret

@@:
  push ebx
  mov ebx, 1
  mov ecx, 1

@@:
  lea eax, [ebx+ecx]
  cmp edx, 3
  jbe @f
  mov ebx, ecx
  mov ecx, eax
  dec edx
  jmp @b

@@:
  pop ebx
  ret

What this code does is calculate the nth Fibonacci number. eax , ebx , ecx and edx are registers in the CPU that store data for quick processing. The code uses these registers to store the answer to intermediate steps of the Fibonacci sequence, pulls that data out of the registers to do computations on them, and then spits out the answer into the ebx register.

On the same Wikipedia page, you’ll find the same Fibonacci calculator written in C (I’ve modified the variable names):

unsigned int fib(unsigned int n) {
  if (n <= 0) return 0;
  if (n <= 2) return 1;

  unsigned int first_number, second_number, current_total;
  first_number = 1;
  second_number = 1;
  while (1) {
    current_total = first_number + second_number;
    if (n <= 3) return current_total;
    first_number = second_number;
    second_number = current_total;
    n--;
  }
}

Here, instead of manipulating data in registers in the CPU, the code simply uses the variables first_number, second_number and current_total, much like you would use them in an algebra problem. Where in the CPU does the code keep the values of the variables first_number, second_number and current_total? You don’t know, because not knowing makes your life easier. You get to refer to variables based on what you decide they’re called, not based on where they’re stored in the CPU.

In C, register allocation is abstracted away. A C programmer doesn’t have to think about it. When they’re done writing their C code, they compile it using a C compiler, and the C compiler will take care of which variable goes into which register. This is part of what makes C a higher-level language than assembly: there is a higher level of abstraction. Many other languages are higher-level still, and abstract away even more of the underlying CPU architecture.

Remember Guttag’s statement on abstraction: “The essence of abstractions is preserving information that is relevant in a given context, and forgetting information that is irrelevant in that context.”

The values of the variables are relevant to our computation, so we want to keep them in our code. Their locations in the CPU are irrelevant to our computation, so we want to forget them. We want to abstract them away.

Abstraction and the real world, with a transport-related aside

Abstraction has costs. A high-level programming language allows for efficient thought, at the expense of efficient operation. The process of compiling, of turning high-level code into machine code, introduces inefficiencies; the compiler will do some things in a suboptimal fashion. However, the efficiency gained by working in a high-level programming language typically far outstrips the efficiency lost by suboptimal machine code.

A related type of cost is the leaky abstraction. One summer in college, I read the entire back catalogue of Joel Spolsky’s blog Joel on Software, where in a well-known post, he laid out the Law of Leaky Abstractions: “All non-trivial abstractions, to some degree, are leaky.” In effect, this means that however you build your abstraction layer, something that you’ve abstracted away will turn out to be important; the abstraction will leak, and the illusion that the abstraction perfectly represents the underlying architecture will be broken.

Modern life is full of abstractions, most of them leaky. Think about a subway map. Here’s Singapore’s:

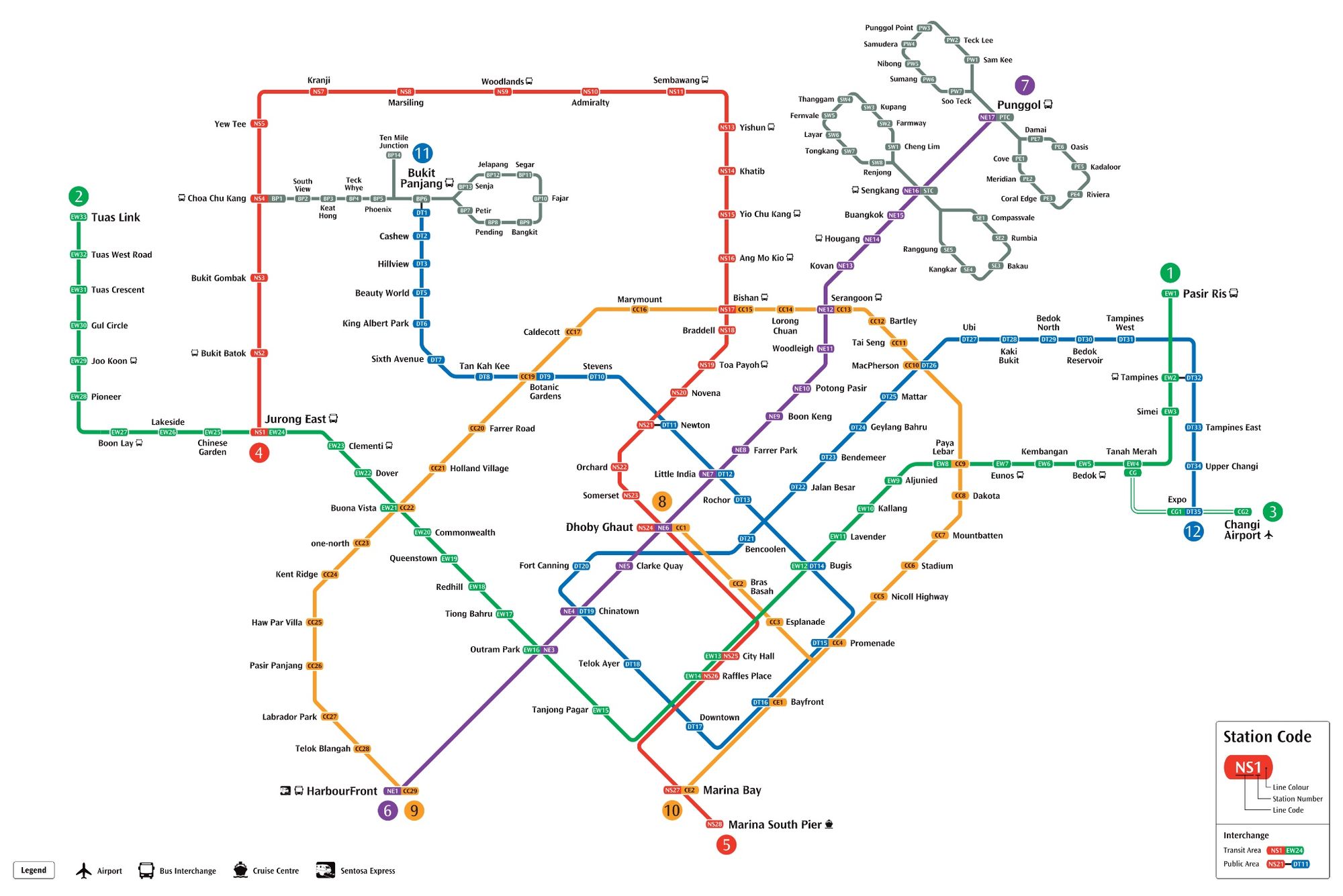Map from Singapore’s Land Transport Authority website

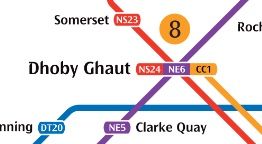
Look at this section:

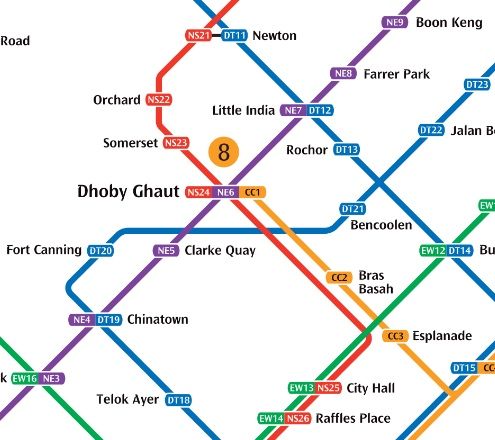Close-up of the MRT map around Dhoby Ghaut

City Hall, Dhoby Ghaut and Newton are all are interchanges. City Hall is as good an interchange as I’ve ever seen in all my travelling: you get out of one train, cross the platform, and get onto the other train. That’s it. No stairs, no escalators, no long walkways. The abstraction is relatively leak-proof.

At Dhoby Ghaut, there’s a maze of escalators and travellators to bring you from one line to another. If you’ve ever travelled by subway in a city with a large subway system, you know this type of station (think Times Square in NYC, King’s Cross in London, or Friedrichstrasse in Berlin). The subway map simply indicates this as an interchange, but it’s not a pleasant experience changing at Dhoby Ghaut. The abstraction is a little leaky now.

At Newton, you have to exit the fare gates, walk a few metres inside the station, and re-enter the fare gates on the other side. This is a bigger leak still. And, if you look at the first map, there’s a similar interchange at Tampines. In the case of Tampines, you have to leave the station, walk outside, and re-enter what is effectively a different station a few hundred metres away.

Why? Subway maps are abstractions, and one of the things subway maps abstract away is the inconvenience of changing lines at interchanges. The East-West (green) and North-South (red) lines were built first, so the interchanges had the benefit of being designed based on the abstraction of the interchange and minimising the difficulty of changing lines.

The North-East (purple) and Circle (yellow) lines were built next, and because they had to be built around the pre-existing lines and any buildings that had sprung up in the meantime, connecting the new lines to the system required a series of walkways and escalators. The physicality of the train lines and the space they needed could no longer be abstracted to the same degree as they were with the first two lines.

Finally, the Downtown (blue) line was built. In order to connect the Downtown line with the other lines in the system, the abstraction of the interchange had to be massaged even further, because the walkways to connect existing train lines to the Downtown line could not even be made to reasonably fit inside the fare gate boundaries. The abstraction of the interchange has sprung a leak, and the subway map reflects it accordingly by altering the graphic design of the interchange stops:

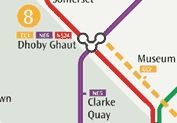Interchange symbol on 2005 map

Interchange symbol on 2017 map

Public area interchange symbol on 2017 map

Leaky abstractions are bad from an operational point of view. They’re suboptimal, and they re-introduce irrelevant information into the system. When looking at the subway map and trying to figure out how to get from station A to station B, you don’t want to think about how far you have to walk at an interchange, how long the transfer might take, or whether you have to leave the station — all of which are really just additional abstractions on top of other things you don’t want to think about, like how much clearance a subway tunnel needs or how wide a walkway has to be to accommodate a rush-hour crowd.

On the other hand, leaky abstractions are intellectually a lot of fun. They reveal a great deal about the underlying structure of a system, all the layers below the leaky layer, and what information is in fact relevant and when. There’s a lot of stuff that you can abstract away for convenience, but that you still need to understand in order to fully grasp a system, and leaky abstractions show you where those things are.

Abstraction in other disciplines

I probably didn’t need to go into such detail, but I wanted to. Understanding abstraction in computing is how I came to understand abstraction more broadly as a concept, and I wanted to lay out some of the key principles of abstraction first, before I moved on to talking about abstraction in other fields.

Part of the reason abstraction is such a prominent idea in computer science, and a relatively poorly developed concept in other fields, is that people who work with computers professionally are taught explicitly about abstraction, early and often. Abstraction simplifies things for the coder. It helps to make tedious and repetitive code clean and elegant. It allows human beings to build complex applications, whether that’s Final Cut Pro or Player Unknown’s Battlegrounds, without having to reinvent the wheel or the half-adder (okay, that’s a really clumsy metaphor).

Conversely, in most of the typical liberal arts fields, abstraction is a relatively modern development in the history of their disciplines. Abstract art and abstract music, for example, only took root at the end of the 19th century, and diverges sharply from its predecessors in terms of beliefs and operating principles. Abstraction in these fields is, at best, one of many modes of operation, and at worst, a punchline. (I’ll admit I’ve done it too; I’ve definitely used Mark Rothko and Richard Serra as punchlines.) Understanding abstraction in computing, though, helped me to understand what it was that artists like Paul Klee and musicians like Arnold Schoenberg did that was so groundbreaking.

One of the things I want to do on this blog is to discuss how ideas and methods from one discipline can be relevant in other disciplines. This is where I’ll start: layers of abstraction. In the coming posts, I’ll be talking about abstraction in other fields, such as art, music, design, and linguistics.